BRAD UY AND JAMES METZ

Triangular numbers have their name because a triangular number of circles can be arranged in the form of an equilateral triangle, as shown in Figure 1.

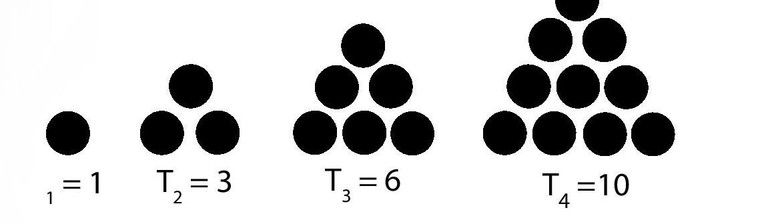
Figure 1. Triangular numbers represented by circles

The first triangular numbers are 1, 3, 6, 10, 15, 21, … At step number 2 we add 2 more circles, at step number 3 we add 3 more circles, so in general at step number n we add n more circles. This is how we generate triangular numbers, but if we wanted to know the tenth triangular number we need to know the ninth triangular number. We need a general formula to find the nth triangular number without knowing the previous one. The general formula for the nth triangular number is Tn = n(n + 1)/2. (For example, T10 =10(9)/2 = 45.) This formula has a nice geometric representation as the area of a right triangle with legs n and n + 1. See Figure 2. Since n(n + 1)/2 = (n2 + n)/2, the nth triangular number is also the average of n and n2 .

Keywords: Special numbers, triangular numbers, tetrahedral numbers, geometry, visualisation

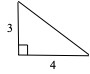
Area = 3•4/2 = 6 = T3

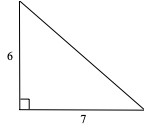
Area = 6•7/2 = 21 = T6

Figure 2. Right triangles whose legs are consecutive positive integers

While triangular numbers can be represented as circles arranged in the form of a triangle, tetrahedral numbers can be seen as a form of a tetrahedron, a pyramid with a triangular base, as in Figure 3. We create tetrahedral numbers by stacking spheres, with a triangular number of spheres in each layer. Figure 3 shows the sum of the first three triangular numbers, 1 + 3 + 6 = 10, the 3rd tetrahedral number.

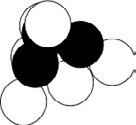
Figure 3. Stacked spheres showing the 3rd tetrahedral number, 10

The first tetrahedral numbers are 1, 4, 10, 20, 35, 56, … While the model does provide motivation for naming the total number of spheres as tetrahedral numbers and it is a nice visual representation of the relationship between triangular numbers and tetrahedral numbers, it does not help us find the nth tetrahedral number unless we know the one before it. As with triangular numbers, we want a general formula to the nth tetrahedral number. This formula for the nth tetrahedral number is Tn = n(n+1)(n+2)/6. (For example, T5 = 5(6)(7)/6 = 35.) Wouldn’t it be nice if we could picture this expression geometrically using a tetrahedron?

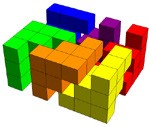
Figure 4. Each of the 6 identical pieces has 10 cubes.

The numerator of the expression that generates tetrahedral numbers is the product of three consecutive positive integers which is conveniently also the volume of a rectangular solid whose dimensions are three consecutive positive integers. Thus, 1/6 of the volume of such a rectangular solid is always a tetrahedral number. For example, a rectangular solid with dimensions 3 × 4 × 5 has a volume of 60, so the third tetrahedral number is 60/6 = 10. Figure 4 shows 6 sets of 10 cubes, each with a unique colour for each set. These 6 sets fit together to form a 3 × 4 × 5 rectangular solid. It is not necessary that cubes in a set be joined or even that cubes of the same colour stay together (the cubes may be anywhere in the solid), but this configuration nicely reveals the triangular numbers 1, 3 and 6 used to generate the tetrahedral number 10. An alternative model is shown in Figure 5, a model suggested by Swati Sircar of Math Space, Azim Premji University.

Step 1. Each of the two sets has 6 + 3 + 1 = 10 blocks for a total of 20 blocks.

Step 2. The bottom 6 blocks in each set join to make a 3 by 4 rectangle; the middle 3 join to make a 2 by 3 rectangle; the top block in each set join to make a 1 by 2 rectangle.

Step 3. Three identical sets of 20 blocks. Step 4. Two sets are joined.

Step 5. The three sets are joined together to form a 3 × 4 × 5 rectangular solid.

Figure 5. Swati’s Construction

This model starts with the formula and fits the model to the formula, so this method does not answer the question, “Why 6?”

We now turn our attention to the possibility of picturing this expression geometrically using a tetrahedron. We must be clear that this is not an effort to develop the formula for the nth tetrahedral number, but rather to show a way to see the expression in a tetrahedron, and notably to account for the number 6 in the expression. We again observe that the nth tetrahedral number is the sum of the first n triangular numbers. For example, the sum of the first five triangular numbers, 1 + 3 + 6 + 10 + 15, is 35, the fifth tetrahedral number.

The formula for the volume of a tetrahedron is Bh/3, where B is the area of the base and h is the height. If a tetrahedron has a right triangular base with legs n and n + 1, the area of the base is n(n + 1)/2, a triangular number. If the height of the tetrahedron is n + 2, then the volume of the tetrahedron, is [(n(n + 1)/2)(n + 2)]/3) or n(n+1)(n+2)/6. See Figure 6. Thus, when asked to determine the nth tetrahedral number, we simply compute the volume of a tetrahedron. For example, the fifth tetrahedral number is Bh/3 = [[(5)(6)/2])7]/3 = 35.

We can now answer, “Why 6?” We have a divisor of 2 from the formula for the area of the triangular base and a divisor of 3 from the formula for the volume of a tetrahedron and hence the divisor is 6.

On the first day of Christmas My true love gave to me A partridge in a pear tree.

On the second day of Christmas My true love gave to me Two turtle doves, And a partridge in a pear tree. n + 2

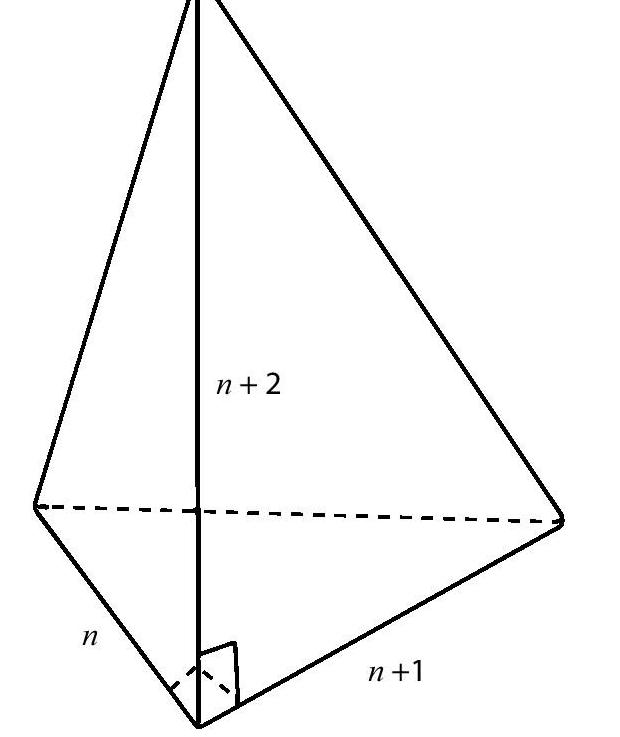
Figure 6. The volume of this tetrahedron is the nth tetrahedral number.

We conclude with a final thought. A popular song in some parts of the world is “The Twelve Days of Christmas,” whose first three verses are:

On the third day of Christmas My true love gave to me Three French hens, Two turtle doves And a partridge in a pear tree.

This pattern continues for a total of twelve days. The number of gifts received each day is a triangular number, so the total number of gifts is the twelfth tetrahedral number, the sum of the first twelve triangular numbers, 364. The song and lyrics are widely available and provide a nice introduction to the problem.

Reference

1. Jim Delaney “Geometric Proof of the Tetrahedral Number Formula” https://demonstrations.wolfram.com/Geometric ProofOfTheTetrahedralNumberFormula/ Published March 7 2011

Brad Uy Brad.uy@gmail.com hails from the beautiful islands of Hawaii and is a creative and light-hearted educator. He has taught maths and English for 15 years, and has volunteered on 8trips with Teachers Across Borders – Southern Africa. He currently teaches Algebra 1 at Kamehameha Schools Kapālama on O`ahu, an educational institution dedicated to serving native Hawaiian children. For recreation, Brad enjoys reading, tennis, cooking, and coffee. Brad may be contacted at

James Metz, is a retired mathematics instructor. He volunteers for Teachers Across Borders -Southern Africa for one month each year and enjoys doing mathematics. James may be contacted at