JAMES METZ AND BRAD UY

Keywords: Age, pattern, relationships.

Our friend Laurie was born in 1962, and this year she will turn 62 years old. We found this interesting. We told her this is her ‘Special Year.’ We then wondered how individuals can determine their Special Year, the year in which the last two digits of their birth year match their age, given their birth year, b. The interested reader may explore this before continuing reading.

For Laurie, one can easily see that in her Special Year, her age is the difference between her birth year and 1900. We simply add that difference (the last 2 digits of her birth year) to her birth year to find her Special Year. Thus, we can know quickly that since Laurie was born in 1962 her Special Year is 1962 + 62 or 2024 and that she will be 62 years old then.

In general, consider a person born in year b between 1900 and 1999, inclusive. A person a years old in their Special Year, S, has the last two digits of their birth year b – 1900 = a, and since S = b + a, by substitution, S = b + (b – 1900). A person born in 1949 was 49 in 1998, so 1998 is their Special Year. For a person born between 1900 and 1999, who is a years old, their Special Year S can be calculated as 1900 + 2a. Since 1900 and 2a and are both even, the Special Year S, must always be an even-numbered year. (See Figure 1.)

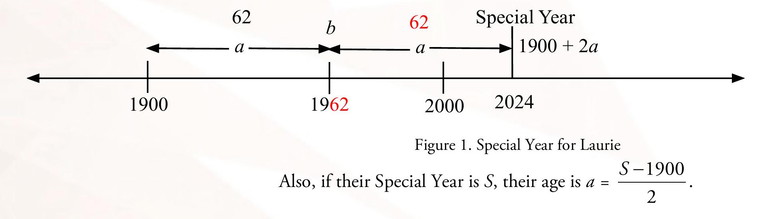
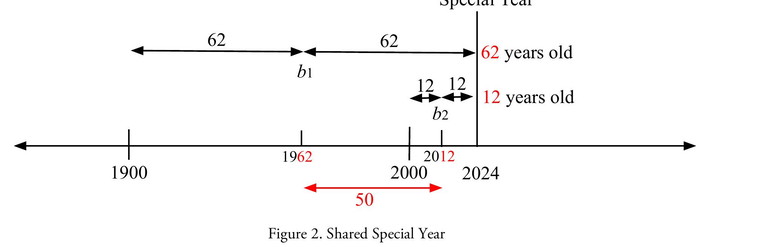
For a person born in 1900, their Special Year is their birth year, 1900. The Special Year of a person born between 2000 and 2099 is S = b + (b – 2000). If a person born between 1900 and 1999 has Special Year S1 and a second person born between 2000 and 2099 has Special Year S2 then they share the same Special Year if S1 = S2 , so b1 + (b1 – 1900) = b2 + (b2 – 2000),

so b2 – b1 = 50, and thus a1 – a2 = 50.

In general, if the difference of the ages of two people born in consecutive centuries is 50 years, then they share the same Special Year. Thus, Laurie (as well as everyone born in 1962) and everyone born in 2012 share the same Special Year, 2024. Such are Special Years in the Common Era. (See Figure 2.)

Pythagoras was born in the year 570 B.C.E. In his Special Year he was a years old, so the last two digits of his birth year b – 500 = a. Since S = b – a, by substitution, S = 500. Surprise! Not only Pythagoras, but everyone born between 599 and 500 had the same Special Year, 500 B.C.E. Of course, no one born before the Common Era would even know they had a Special Year unless they used a benchmark of year 1 C.E. as we do. (See Figure 3.)

James Metz, metz@hawaii.edu is a retired mathematics instructor. He volunteers for Teachers Across Borders -Southern Africa for one month each year and enjoys doing mathematics. James may be contacted at

Brad Uy Brad.uy@gmail.com hails from the beautiful islands of Hawaii and is a creative and light-hearted educator. He has taught maths and English for 15 years, and has volunteered on 8 trips with Teachers Across Borders – Southern Africa. He currently teaches Algebra 1 at Kamehameha Schools Kapālama on O`ahu, an educational institution dedicated to serving native Hawaiian children. For recreation, Brad enjoys reading, tennis, cooking, and coffee. Brad may be contacted at