MATH SPACE

Algebra tiles are a generalization of 2D base-10 blocks popularly known as flats-longs-units, or FLU, which were reviewed in the March 2024 issue of At Right Angles [5]. Simply speaking, the ten generalizes to “x” as follows, to form the three basic algebra tiles (with suggested dimensions: x → 2inch and 1 → 2cm):

• The big square, i.e., flat or 100 becomes x2 (x × x or 2inch × 2inch)

• The rectangle, i.e., long or 10 becomes x (x × 1 or 2inch × 2cm)

• The small square, i.e., unit or 1 remains the same (1 × 1 or 2cm × 2cm)

But there is a crucial difference: algebra tiles come in two (contrasting) colours to represent positive and negative versions, i.e., x2 and -x2 , x and -x, 1 and -1 as shown in Figure 1. Most of the virtual (and online) versions show the positive tiles in different colours based on size but all negative tiles in the same colour. Logically, if all negative tiles are in the same colour, then the same should happen for all positive tiles. Mathigon Polypad allows one to make the colours uniform (Figure 1). Another option is to make the tiles double sided so that one side represents a positive tile while the other represents a negative one. There are several advantages to doublesided tiles such as:

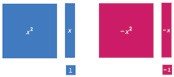
Figure 1

1. These are easier to make from any box with an exterior easily distinguishable from its interior.

2. Only one set of tiles need to be made, instead of two separate sets for positive and negative.

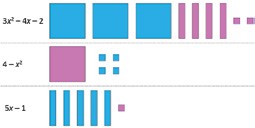
Figure 2

3. Pedagogically speaking, turning over or flipping a tile changes its sign from positive to negative or vice versa. So, flipping a tile is equivalent to sign change. This becomes very useful for subtraction.

Since algebra tiles include negative tiles, an understanding of integers is crucial (see [6]), especially:

A. Zero-pairs: 1 and -1, x and -x, x2 and -x2 which can be brought in and taken out as and when needed as they do not change the expression.

B. Subtracting a quantity is equivalent to adding its additive inverse, for example, subtracting 13, -7, 5x and -2x2 are equivalent to adding -13, 7, -5x and 2x2 respectively.

C. Positive × negative and negative × positive are negative.

D. Negative × negative is positive.

With these six tiles in three sizes, we can show any polynomial (i) in one variable, (ii) of degree 2, (iii) with integer coefficients. Usual algebra tiles do not allow fractional coefficients. Figure 2 represents several such polynomials with blue indicating positive tiles and pink indicating negative. Notice that 4 – x2 is actually 4 + (-x2 ) and 5x – 1 is 5x + (-1). This is why we need the negative tiles.

However, the tiles in Mathigon Polypad can be halved to get x/4, x2 /2, 1/8 etc. Only halving is allowed (horizontally or vertically). So, it is not possible to show x/3, x2 /5, 1/6 etc. (Figure 3).

Another crucial difference between FLU and algebra tiles is the absence of exchange. In the case of FLU, it is a universal fact that 10 units make a long, and 10 longs make a flat. However, in the case of algebra tiles, since the value of x is not known or can have many possibilities, we do not know how many 1s are equivalent to an x. Therefore, there is no exchange among the tiles. This is similar to why the terms in a polynomial do not collapse into one term. So, the tiles reinforce the notion that polynomials like 3x2 – 2x – 5 cannot be simplified further.

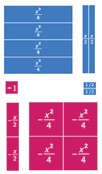
Figure 3

As we represent polynomials using algebra tiles, a few things automatically become clear:

• Why x2 is called x-squared and how it is linked to the geometric square.

• The difference between x2 , i.e., x × x as one square tile vs 2x, i.e., x + x as two rectangular tiles.

• The notion of like terms – one can count tiles of the same size, can even remove zero-pairs but cannot combine tiles of different sizes to be expressed as a single term.

Figure 4

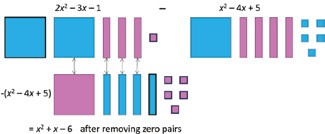
Figure 5

Since the relation between x and 1 is unknown, there is no way to compare two polynomials. However, we can add and subtract any two polynomials as long as they can be represented by the tiles.

The rules of addition are similar to that for whole numbers with FLU: 1. Make each polynomial with the tiles. 2. Combine tiles of the same size and discard any zero-pair. 3. The remaining tiles represent the sum.

Similarly, the steps for subtraction, i.e., p(x) – q(x) are: 1. Make the polynomials p(x) and q(x). 2. Flip the tiles of q(x) to get -q(x) 3. Add p(x) and -q(x), i.e., combine tiles of same size and discard any zero-pair. 4. The remaining tiles represent p(x) – q(x) = p(x) + [-q(x)]

It is possible to execute a subtraction p(x) – q(x) in a different way, that is closer to the whole number process:

1. Make the polynomial p(x) 2. Imagine the polynomial q(x) 3. Add zero pair(s) to p(x) as needed so that there is enough to subtract q(x) [i.e., remove x2 , -4x and 5] 4. Subtract q(x) from p(x), i.e., remove tiles as mentioned above, what remains represents p(x) – q(x)

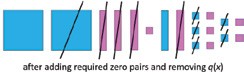
Figure 6

(2x2 – 3x – 1) – (x2 – 4x + 5) =x2 +x – 6

Figure 4 shows the sum of two polynomials and Figure 5-6 illustrate the difference of two polynomials.

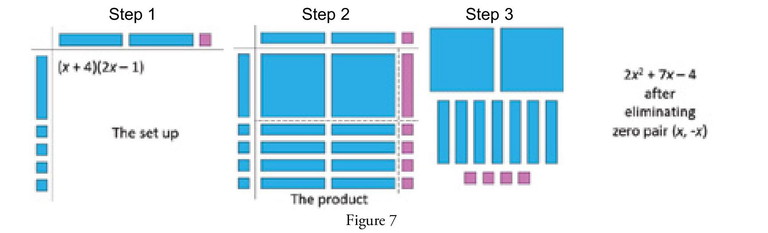
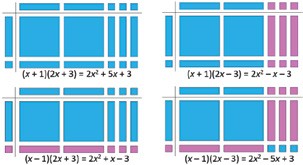
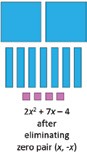
Figure 8

However, this can be quite cumbersome since it may need zero pairs of more than one type (1 and -1, x and -x, x2 and -x2 ). Moreover, given B, i.e., subtracting a term is equivalent to adding its additive inverse, every subtraction can be considered as an addition. Therefore, flipping q(x) is a simpler option for polynomial subtraction.

Multiplication-division are similarly restricted to polynomials of a maximum degree of 2. The product of two linear polynomials using algebra tiles is very similar to the product of two 2-digit numbers. Note the four regions of big and small squares and horizontal and vertical rectangles in Step 2: The product of Figure 7. The steps for multiplication are:

1. Arrange one factor polynomial along the left border and the other on the top border. 2. Fill the array, matching each dimension of each tile with the borders. 3. Remove any zero-pairs [Where can the zero-pairs occur in a product? Check Figure 8].

Figure 8 represents all possible combinations in terms of signs keeping the leading terms positive. Note the cases where zero-pairs occur. Consider the similarities and differences among these four cases. This understanding is crucial for middle term factorization. And yes, algebra tiles do a fantastic job of exploring that!

Figure 9

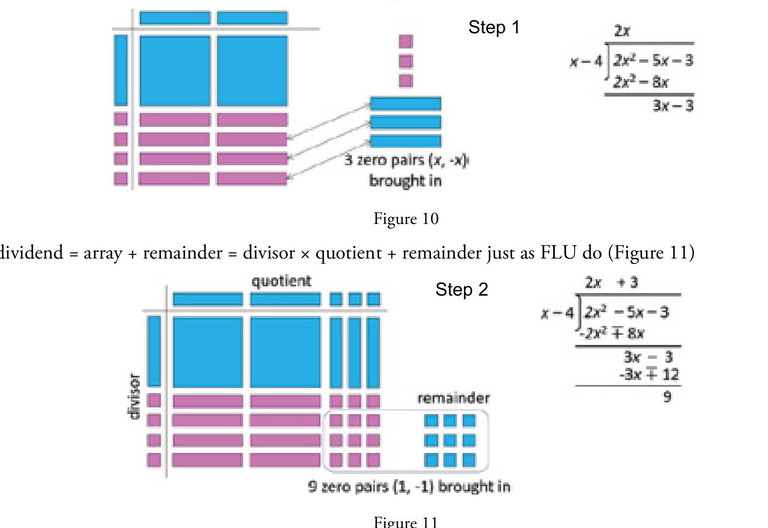
Division of a degree 2 polynomial by a degree 1 polynomial with algebra tiles (Figure 9) is also very similar to dividing a 3-digit number with a 2-digit number with FLU. See [5].

Step 1: Place the x2 tiles to get the partial quotient 2x and complete the step by bringing in three zero pairs (x and -x), 3x – 3 remains (Figure 10)

Step 2: Place the x tiles to get the remaining partial quotient 3 and complete the step with nine zero pairs (1 and -1), 9 is the remainder and 2x + 3 is the quotient (Figure 11)

Note how the dividend is in two parts at the end – the array and the remainder, i.e.,

In addition, the algebra tiles can be used to represent all the quadratic identities:

• (a + b)2 and related

• (a – b)2 and related

• (a + b)(a – b)

• (a + b)2 + (a – b)2

• (a + b)2 – (a – b)2

So, as far as polynomials are concerned, algebra tiles help significantly. However, physical (or virtual) tiles have fixed dimensions. So, these are not great for equations. It may be possible to explore linear and quadratic equations in one variable with algebra tiles. We are yet to explore that in depth.

Some versions include one more variable y and tiles of three more sizes, viz., y 2 , xy and y (Figure 12). This allows polynomials in two variables, but the remaining restrictions of degree and coefficients remain. We are yet to explore if these extended algebra tiles, especially, y along with x and 1, can provide some pedagogic advantage for say simultaneous linear equations in two variables.

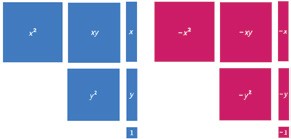
Figure 12

It is possible to address polynomials of degree 3 with cuboids. But it will be quite cumbersome and would definitely need two sets of cuboids – positive and negative – since the “flipping” advantage is lost with the 3rd dimension. Moreover, the cuboids may not provide additional pedagogic benefits to counter the effort.

Last but not the least, it is perfectly ok to introduce the tiles to students with no exposure to FLU. The tiles are a generalization of FLU and the transition from FLU to algebra tiles can help one see how whole numbers are simply ‘polynomials in ten’ with the digits as coefficients. But FLU is not a prerequisite for algebra tiles. However, coloured counters for integers are a prerequisite for the tiles (see [6]).

1. How to make algebra tiles: https://bit.ly/4buTsky

2. How to use algebra tiles: https://bit.ly/3zrFVNu

3. Explore algebra tiles virtually: https://bit.ly/3W7x3Wn

4. Algebraic identities with algebra tiles: https://bit.ly/3RSzyt0

5. FLU review: https://bit.ly/3XO1RMX

6. Integers:  https://bit.ly/4bneWQw

7. Mathigon Polypad: https://bit.ly/3XLzU8o

MATH SPACE is a mathematics laboratory at Azim Premji University that caters to schools, teachers, parents, children, NGOs working in school education and teacher educators. It explores various teaching-learning materials for mathematics [mat(h)erials] their scope as well as the possibility of low-cost versions that can be made from waste. It tries to address both ends of the spectrum, those who fear or even hate mathematics as well as those who love engaging with it. It is a space where ideas generate and evolve thanks to interactions with many people. Math Space can be reached at mathspace@apu.edu.in

If we consider different types of quadrilaterals – square, rectangle, rhombus, parallelogram, kite, trapezium, isosceles trapezium, dart (or concave kite) etc., we can easily state the kind of symmetry each type has. For example, rhombus and rectangle, each have a line of symmetry and rotational symmetry of order 2.

But what happens when we flip the question: 

A. If a quadrilateral has line symmetry, what kind of quadrilateral is it? 

B. If a quadrilateral has rotational symmetry, what kind is it?

Flipping a question provides scope for mathematical exploration, giving students opportunities to develop observation, documentation and analytical skills while honing their conceptual understanding. We invite responses from readers - send them to AtRightAngles.editor@apu.edu.in And we promise our take in the November issue!

At Right Angles is a quality resource dedicated to mathematics education in India’s public education system. It is specifically designed for teachers and teacher educators at the foundational, preparatory, and middle school levels.

We invite articles from mathematics teachers, educators, practitioners, parents, and students. If you are looking for a platform to contribute articles that support and enhance the learning experience of mathematics particularly for students approximately in the age group 6-14 years, we welcome your submissions.

SUGGESTED TOPICS AND THEMES

Submitted articles should focus on curricular content applicable to Classes 1-8 and could:

• Explain and illustrate themes and topics outlined in the National Curriculum Framework for School Education 2023 (NCF-SE 2023).

• Specifically address challenges discussed in the NCFSE 2023.

• Be substantiated accounts of the history of mathematics or the history of mathematical thinking.

• Include innovative worksheets or methods to engage students in drill and practice.

• Describe real-life applications of mathematics relevant to the child’s context.

• Describe interdisciplinary activities or projects.

• Review puzzles or games with a practical connection to the syllabus.

• Offer guidance on selecting relevant content, including online resources.

• Develop pedagogical strategies for foundational numeracy as well as computational thinking.

• Assist teachers in implementing differentiated teaching practices.

• Review of Teaching Learning Material (TLM) or describe how to use local context, and local TLM in the math class.

• Provide material to help students bridge gaps in conceptual understanding.

• Address issues in assessment.

• Suggest ways to identify and address misconceptions in mathematics learning.

• Offer a list of problems along with discussions on their solutions and problem-solving strategies that are not commonly found in textbooks.

In addition to full-length articles, we also welcome shorter pieces that can include a variety of engaging content. These could be reviews of books, mathematics software, or YouTube clips that explore mathematical themes. Other contributions can be ‘proofs without words’, mathematical paradoxes, ‘false proofs’, or creative expressions such as poetry, cartoons, or photographs with a mathematical theme. We also welcome anecdotes about a mathematician or interesting examples of ‘math in craft, movies, etc.’.

Articles may be sent to  AtRightAngles.editor@apu.edu.in

Please refer to specific editorial policies and guidelines on the following page.

Policy for Accepting Articles

At Right Angles is an in-depth magazine on matters of consequence to early mathematics and mathematics education. Hence articles must attempt to move beyond common myths, perceptions, and fallacies about mathematics.

The magazine has zero tolerance for plagiarism. By submitting an article for publishing, the author is assumed to declare it to be original and not under any legal restriction for publication (e.g. previous copyright ownership). Wherever appropriate, relevant references and sources will be indicated in the article.

At Right Angles brings out translations of the magazine in other Indian languages. Hence, Azim Premji University holds the right to translate and disseminate all articles published in the magazine.

If the submitted article has already been published elsewhere, the author is requested to seek permission from the previous publisher for re-publication in the magazine and mention the same in the form of an ‘Author’s Note’ at the end of the article. It is also expected that the author forwards a copy of the permission letter, for our records. Similarly, if the author is sending his/her article to be re-published, (s)he is expected to ensure that due credit is then given to At Right Angles.

While At Right Angles welcomes a wide variety of articles, submissions that are found relevant but not suitable for publication in the magazine may be used in other avenues of publication within the University network, with the author’s permission.

Keywords: TLM, modelling, algebra tiles, representation, algebraic operations