MATH SPACE

How do we multiply two numbers like 84 × 67? At the first step we find 84 × 7. This involves a ‘carryover’, or regrouping, i.e., 84 × 7 = (4 + 80) × 7 = 4 × 7 + 80 × 7. So,

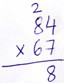
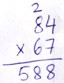
Figure 1

• We start with 4 × 7 = 28

• And put down 8

• Remember that we need to add 2 to the next product

• Find 80 × 7, or rather 8 × 7 = 56

• And add 2 to this, i.e., 56 + 2 = 58

• Complete the product 84 × 7 = 588 And this is just step 1 (Figure 1)!

Note the complexity! When we add, we deal with only one operation and all digits are added. Here on the other hand, to multiply by a 2-digit number, one has to multiply 8 and 7 and then add 2. In other words, there are two operations in this step – multiplication and addition. Therefore, the order of these two operations matters since (7 × 8) + 2 ≠ 7 × (8 + 2). But it is quite natural for a learner to get confused on whether to multiply (by 7) first and then add, or the other way. Also, unlike addition, the ‘carry’ is not usually written down. So, there are more things to keep in mind.

A similar set of steps is repeated for 84 × 60, or 84 × 6 = 504. This also requires ‘carry’ and since writing multiple such digits can be confusing, none are usually written. But that hardly helps a learner at the beginning.

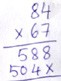
Figure 2

Moreover, this is often written with a blank or ‘×’ at the unit’s place (Figure 2). Then we add up 588 and 504×. No one is taught to add 8 + × but is expected to do so here. It is surprising how this continues in classrooms still, at least 20-25 years after textbooks have changed. Since we are multiplying by a multiple of 10, i.e., 60 in this case, why shouldn’t we write the partial product of 84 × 60 as 5040? We hope that teachers stop using the ‘×’ out of sheer inertia to change and make their pedagogy more meaningful.

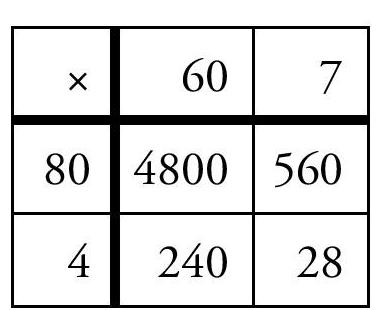
figure 3

For a 3-digit × 3-digit product, say 379 × 825, this would become Figure 4. However, as the number of digits increases, writing all the zeros may become cumbersome. But there is a way out as well!

We can use a smaller lattice, e.g., Figure 5 for 84 × 67. But to keep track of the zeros in the partial products (as shown in the big lattice in Figure 3), it helps to diagonalise each cell (Figure 6).

Is there another way to avoid such issues?

Fortunately, there is one. And it can be used for any multiplication with two whole numbers, no matter how large each is.

The standard method, illustrated above uses distributive property only once, viz.,

84 × 67 = 84 × (7 + 60) = 84 × 7 + 84 × 60

which results in the two partial products 588 and 5040 that gets added at the end.

However, we can use the distributive property twice, i.e., for both numbers and get four partial products:

84 × 67 = (80 + 4) × (60 + 7) = (80 × 60) + (4 × 60) + (80 × 7) + (4 × 7)

This can be tabulated very nicely in a 2-way table (Figure 3). And then the partial products can be added up. Note that this is not radically different from the earlier method.

The column-wise sums are the same partial products which we got earlier.

Note how the digits in each diagonal (bottom-left to top-right) correspond to the digits in the sum of partial products (right to left) as shown in Figure 7. This is explained if we use arrow cards to make the big lattice and colour the small one accordingly (Figure 8). Figure 7 So, we could sum up diagonally as well (Figure 9).

Therefore, if we crystalize this method, it boils down to:

• Create a 2-way table with the numbers to be multiplied

• Draw diagonals in each cell

• Multiply digit-by-digit to fill each cell

• Add along each diagonal group of digits starting from the bottom-right•

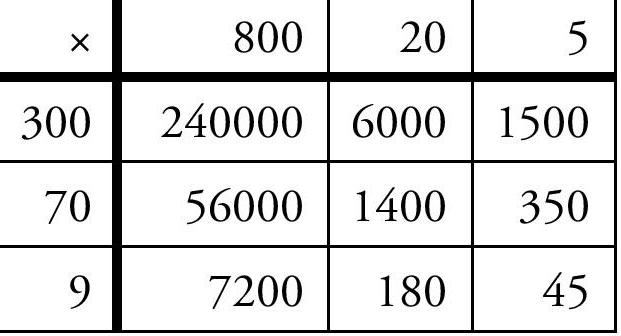
Figure 4

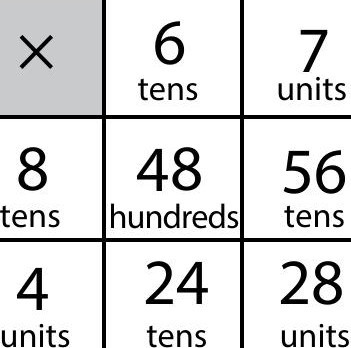
Figure 5

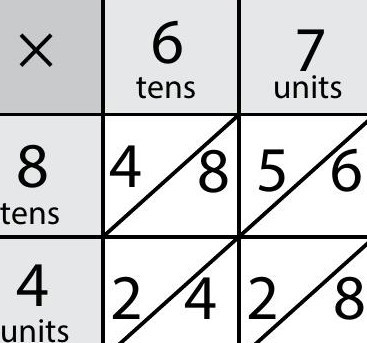
Figure 6

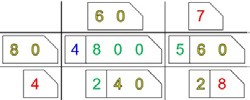
Figure 8

Figure 9

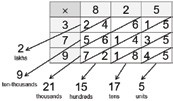
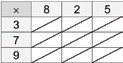
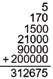
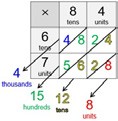
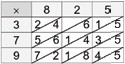
Figure 10

Note that in this method, when we multiply, it is just digit-by-digit multiplication with no addition, and therefore no ‘carry’ or regrouping. And once all multiplication is done, we add up. So, this is a written process like the previous one. But without the juggling of multiplication and addition. And no chance of any “×” instead of 0 (as placeholder).

However, pedagogically speaking, one should always start with the big lattice and then transition to the small one using arrow cards. It helps a lot to start with some 2D base-10 blocks aka flatslongs-units (FLU), reviewed in the Mar 2024 issue of this magazine [3], for up to 2-digit × 2-digit products. But for bigger ones it helps to draw lines and count the number of intersections. The lines should be colour-coded to separate ones from tens, etc. Number of intersections of each type can be used to fill the 2-way table with diagonals. We illustrate this for 379 × 825 (Figure 11). [Drawing intersecting line for multiplication is popularly known as lattice method.]

Figure 11

The need to multiply big numbers by hand has certainly reduced in real life thanks to the prevalence of technology. However, at school and therefore in board exams, learners have to multiply multi-digit numbers by hand. Various problems in percentages and mensuration may require computing such products. We hope that this method provides a simpler way to do that compared to the standard process.

1. Initiating multiplication (ppt): https://bit.ly/3L8CGgs

2. Lattice multiplication (ppt): https://bit.ly/3W6NjGY https://bit.ly/3RM3W87

3. Flats-Longs-Units (review):

MATH SPACE mathspace@apu.edu.in is a mathematics laboratory at Azim Premji University that caters to schools, teachers, parents, children, NGOs working in school education and teacher educators. It explores various teaching-learning materials for mathematics [mat(h)erials] their scope as well as the possibility of low-cost versions that can be made from waste. It tries to address both ends of the spectrum, those who fear or even hate mathematics as well as those who love engaging with it. It is a space where ideas generate and evolve thanks to interactions with many people. Math Space can be reached at

Keywords: Multiplication, algorithm, two-digit, lattice, conceptual understanding