Apologies for interrupting your experience.
This publication is currently being maintained by the Magloft team. Learn more about the technology behind this publication.
Manage your subscription to this publication here or please contact the publisher My First Publication for an update.
Mathematical Discourse: Going Beyond Right Answers
PRACHI M
It was a winter day, and all the students gathered on the ground for assembly. The air was filled with the melodious notes of the national anthem and other uplifting tunes, setting the stage for a day of learning. As the last strains of music faded away, the teacher asked, “Who will tell me the table of 14?” Some students raised their hands while some started hiding behind others. “Let’s start from Class 3, Aryan you tell me, what is 14 times 7?” Aryan seemed nervous and though he tried, could not recall what 14 × 7 was. After the assembly, the teacher proudly told me how some of their students could recite the tables till 30. Later, in a fourthgrade class, a student flawlessly solved double digit multiplication but confessed to simply following instructions when asked why he wrote a ‘0’ while multiplying by the second digit. These two anecdotes highlighted for me, how school mathematics often focuses on memorization and question-answer conversations, stifling the joy and creativity inherent in exploring numbers.
What is mathematical discourse?
The communication that occurs in a mathematical classroom is known as mathematical discourse. In most classrooms ‘correcting discourse’ is mostly used, in which the communication stays limited to students answering the teacher’s questions and the teacher saying whether the answer is correct or wrong. Only the prescribed method is followed by the students in order to arrive at the ‘correct answer’, leaving no scope to explore the process. However, the goals of mathematics education aim to develop logical thinking, explaining patterns, making, refuting, and proving conjectures, problem-solving, computing fluently, and communicating clearly and precisely.
Keywords: Communication, exploration, reasoning, understanding, courtesy.
Good mathematical discourse happens when students share their ideas and listen to each other’s mathematical thoughts instead of the teacher dominating the communication. This helps them understand mathematics better because they see different ways of thinking about problems. It also helps them feel more confident in their mathematics skills as they become better at understanding and explaining concepts. This helps teachers too as they can see what students understand and what they don’t, so they know how to help them learn better.
My experience of setting mathematical discourse in a classroom
An attempt to promote mathematical discourse was made while working on number sense with elementary grades. Certain rules and norms such as listening to others, respecting others’ opinions, justifying one’s own opinion, etc. were set for our mathematics classroom. The key rule that was set while establishing the discourse was: don’t just say the right answer but tell us how you approached the problem. Two strategies which were questioning and explaining mathematical thinking were widely used in this process. Different structures such as one-to-one conversations, working in pairs, working in groups, and wholeclass discussions were used at different times. Students also used different representations and models while explaining their mathematical thinking.
While working with students of Class 1, it was initially difficult to get them to talk about what they were thinking. In the initial stage, we had good one-to-one communication. Later, they were also able to engage in communication during group work and whole class discussions. I noticed that the Class 3 students had the urge to either give the right answer or listen passively. So, I made it a practice to follow every answer with the question ‘How did you get it?’ Initially, I saw students struggling to express what they were thinking and end up giving one-word answers. At such times, asking more follow-up questions such as ‘Can you explain this step?’, ‘What do you mean by this?’ etc. really helped. At times reframing what they wanted to say using complete sentences and asking them if that was what they meant, also helped as students were able to edit their responses and clarify their thinking. After a few days of practice, I was delighted when the students started asking their classmates ‘How?’ they got their answers.
In the following examples, probing discourse in which the teacher asks different probing questions as mentioned above, is used to understand student thinking and approach. This type of discourse helps support procedural fluency and conceptual understanding.
One-to-one communication:
While working on addition with Class 1, students were asked to draw different representations to explain their answers to the question:
‘Ramesh has 5 jamun trees, 3 mango trees, and 7 guava trees in his orchard. How many trees are there in the orchard?’
How could you write/draw what you are doing?
Ananya’s representation of the problem is shown in Figure 1.
Teacher: How did you count?
Ananya: I counted one, two, three……fifteen
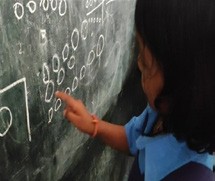
Figure 1
Immediately the teacher understood that she used the ‘count-all’ strategy.
It helps to understand exactly at what level the student is on the learning trajectory and assist them to move upward on it. Following this, we worked on different techniques to help students use more efficient ways of approaching such problems by using a ‘count-on’ strategy.
Communication during pair work:
Students asked their partners different word problems which they had framed themselves. Aryan: If I have 30 chocolates and I gave 6 to Virat, how many chocolates will I have?
Harish: 22... (after some thinking) No no it will be 24.
Aryan: How?
Harish: 6 and 4 is 10. So, if I gave 6 to Virat, I would have 4. And, I have 20 of 30 chocolates, so I will have 20 and 4...24 chocolates.
The above dialogue helped the student to refine his thinking and confidently express his mathematical strategy.


Such discourse helps to identify students’ misconceptions which otherwise go unaddressed. It also helps in developing reasoning, better understanding and confidence in communication.
Communication during whole class discussion:

Figure 2
Teacher: What can you see? (Before this task we worked on ten bonds) Ashu: I can see 3.
Teacher: Yes, there are 3 blue dots. What else can you see?
Soumya: I can see 3 + 2 + 5 = 10
Teacher: How Soumya? Can you explain more?
Soumya: Because there are 3 dots and if we add 2 more, it will be 5 and the remaining 5 would make 10.
Teacher: Yes, so Soumya is saying that if she adds 3 and 2 it will be 5 and adding again 5 will make 10. Do you all agree?
Students: Yes Teacher: What else can we see? Deepa: We can also say 10 – 7 = 3 Teacher: Do you agree with what Deepa said?
2) In Class 3, we worked on using different strategies to engage with double-digit addition. Students were asked to come forward and explain their way of dealing with the problem. The problem was 37 + 24.

Figure 3
Mention the name of the students along with their strategy
Teacher: Can you please explain how you approached the problem?
Rithika: I wrote 37 as 30 and 7, similarly 24 as 20 and 4. I added 30 and 20 which is 50, also added 7 and 4 which is 11. Then I added 50 + 11 which will be 61.
Sarita: I thought of 37 and 10,10,10 and 7. 24 as 10, 10 and 4. Later I added all the 10s and it will be 50. 7 and 4 are 11, so 50 and 11 are 61.
Latika used the same strategy as Sarita. Teacher: What do you think is the most efficient way of approaching the problem? Rahul: I think 10+10+10+…. Used by Latika and Sarita is an efficient one.
Teacher: Okay, so Rahul thinks using ‘breaking into 10s’ and adding is efficient. What do others think?
Sarita: I feel Rithika’s method is more efficient. Teacher: Why do you think so?
Sarita: Because she directly added 30 and 20, and further added 7 and 4 which is more efficient than adding 10 each time.
Suggested questions
Who has a different solution?
Have you thought of another way this could be done?
Whose method do you find more efficient?
The best part of this engagement was students started exploring and figuring out different methods to approach a problem, they provided reasoning for the problems instead of directly writing the answer which was previously valued the most in their classroom. They listened patiently to their classmates and the way they approached the problem. Even for missing number problems students were able to think instead of directly doing the problems mechanically. The below picture shows two methods used by a student for the same problem of missing addend.
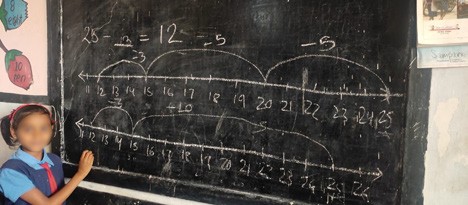
Some points to remember while implementing classroom discourse:
1. It takes time to establish a mathematical discourse-rich classroom but it’s worth all the effort. As students find their voice in the learning process, it makes the learning more meaningful and joyful.
2. One needs to identify and support the one not participating in the discourse as students might find the process overwhelming and need enough encouragement and support during the initial stage.
3. Assessing individual students while setting up such classroom culture could be difficult at the beginning but will get easier with proper planning.
Conclusion:
Mathematical discourse is a powerful tool to bring the required shift from a top-down mathematical learning process to a meaningful mathematical learning process. Fostering mathematical discourse in the classroom is essential for transforming mathematical learning from a passive to an active process in which students take ownership of their learning. By creating environments where students feel valued, supported, and empowered to communicate their mathematical ideas, teachers can nurture confident, rational thinkers and listeners. Despite challenges, the benefits of mathematical discourse outweigh the efforts involved, leading to deeper engagement, richer understanding, and a more inclusive learning community.
References: 1. National Curriculum Framework, 2023. National Curriculum Framework for School Education. 2. National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics.

Prachi M. prachimakde5@gmail.com is a passionate math educator with an M.A. in Education from Azim Premji University. She has been working in the education domain for the last 5 years and strives to make mathematics fun and accessible for all. Prachi may be contacted at