Apologies for interrupting your experience.
This publication is currently being maintained by the Magloft team. Learn more about the technology behind this publication.
Manage your subscription to this publication here or please contact the publisher My First Publication for an update.
Kite Families: An investigation of a family tree!
TearOut
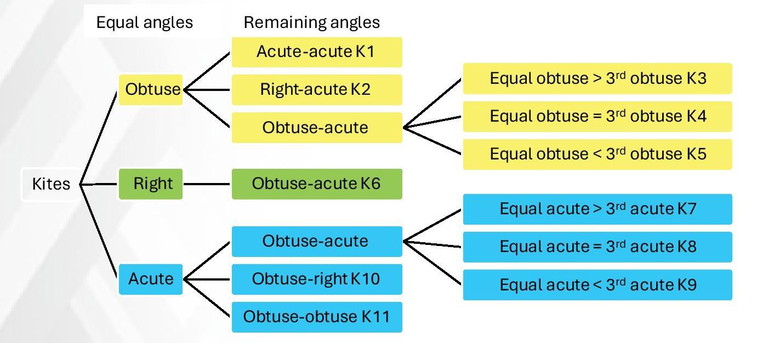
There are 11 types of kites (excluding rhombi) according to the poster.
This poster will help your students make friends with these 11 types. Do give the students time to study it and come up with properties for each of the kites K1, K2… K11. Some important points are given below. Students are sure to come up with these or other points during the discussion, if they don’t then do share at your discretion.
A. Along the line of symmetry
Two possibilities for rhombi:
i. Obtuse-acute, i.e., a non-square rhombus
ii. Right, i.e., square
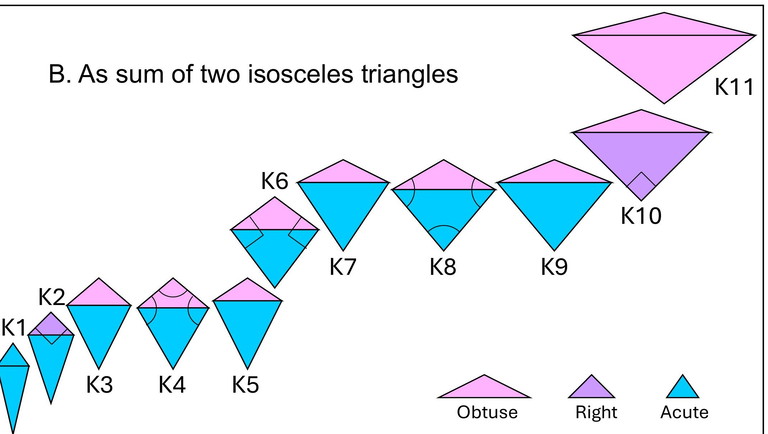
B. As sum of two isosceles triangles
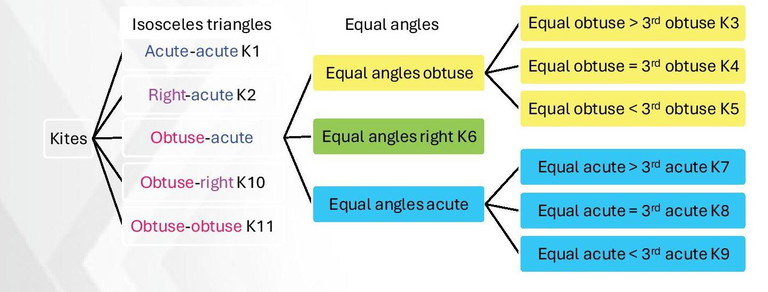
Rhombus: obtuse-obtuse or acute-acute depending upon the choice of diagonal Square: right-right.
Keywords: quadrilaterals, kites, properties, angles, classification, exploration
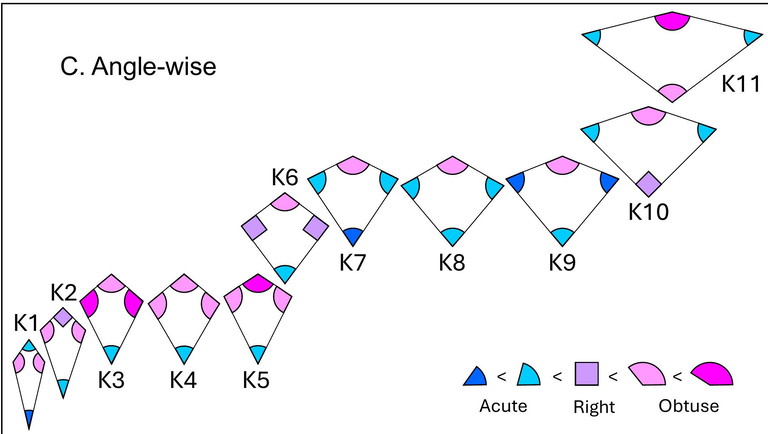
C. Angle-wise
Classification identical to A.
K6 is the only cyclic kite with all four vertices on a circle.
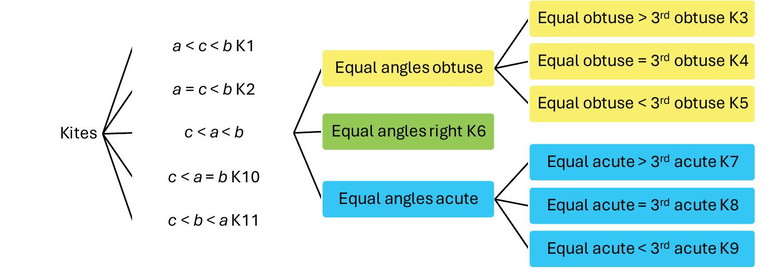
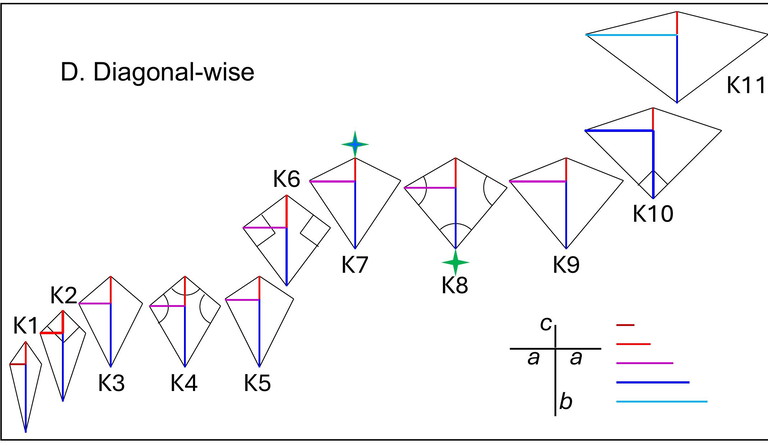
D. Diagonal-wise
Halving diagonal longer for K1, K2… K6
Halving diagonal shorter for K8 (unless square), K9… K11
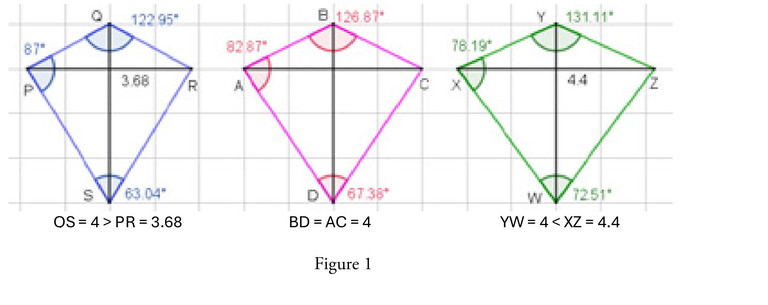
ABCD, PQRS, XYZW are K7 with equal acute angles > 3rd acute ones
Proof:
Consider kite ABCD with AB = BC and AD =DC such that diagonals AC = BD intersect at O.
To show: ∠BCD < 90° Construct circle with diameter BD.
Let the circle intersect OC at X. ∠BXD = 90° since it is an angle in a semicircle.
∠BCO + ∠XBC = ∠BXO (exterior angle equals sum of two opposite interior angles)
⇒ ∠BCO < ∠BXO Similarly, ∠DCO < ∠DXO
∴ ∠BCD = ∠BCO + ∠DCO < ∠BXO + ∠DXO = ∠BXD = 90°
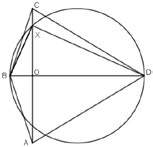
Figure 2
Specific Guidelines for Authors
Prospective authors are asked to observe the following guidelines.
1. Engaging Introduction: Write in a readable and inviting style, aiming to capture the reader’s attention from the start. The first paragraph of the article should convey clearly what the article is about. For example, the opening paragraph could be a surprising conclusion, a challenge, a figure with an interesting question, or a relevant anecdote. Importantly, it should carry an invitation to continue reading.
2. Catchy Title: Title the article with an appropriate and catchy phrase that captures the spirit and substance of the article.
3. Style: Avoid a ‘theorem-proof’ format. Instead, integrate proofs into the article in an informal way.
4. Balance: Refrain from displaying long calculations. Strike a balance between providing too many details and making sudden jumps that depend on hidden calculations.
5. Accessible language: Avoid specialized jargon and notation that will be familiar only to specialists. If technical terms are needed, please define them.
6. Use visuals: Where possible, provide a diagram or a photograph that captures the essence of a mathematical idea. Never omit a diagram if it can help clarify a concept.
7. Concise References: Provide a compact list of references, with short recommendations.
8. Exercises and Questions: Make available a few exercises, and some questions to ponder either in the beginning or at the end of the article.
9. Citation format: Cite sources and references in their order of occurrence, at the end of the article. Avoid footnotes. If footnotes are needed, number and place them separately.
10. Abbreviations and Acronyms: Explain all abbreviations and acronyms the first time they occur in an article. Make a glossary of all such terms and place it at the end of the article.
11. Labelling visual elements: Label and number all diagrams, photos and figures included in the article. Attach them separately with the e-mail, with clear directions. (Please note: the minimum resolution for photos or scanned images should be 300 dpi).
12. Precise references to visuals: Refer to diagrams, photos, figures and tables by their numbers and avoid using references of these kinds: ‘here’, ‘there’, ‘above’, ‘below’, ‘to the left’, ‘to the right’.
13. Author Bio: Include a high-resolution photograph (author photo) and a brief bio (not more than 50 words) that gives readers an idea of your experience and areas of expertise.
14. British Spelling: Adhere to British spellings – organise, not organize; colour not color, neighbour not neighbor, etc.
15. Format for submission: Submit articles in MS Word format or in LaTeX.
Kite Families
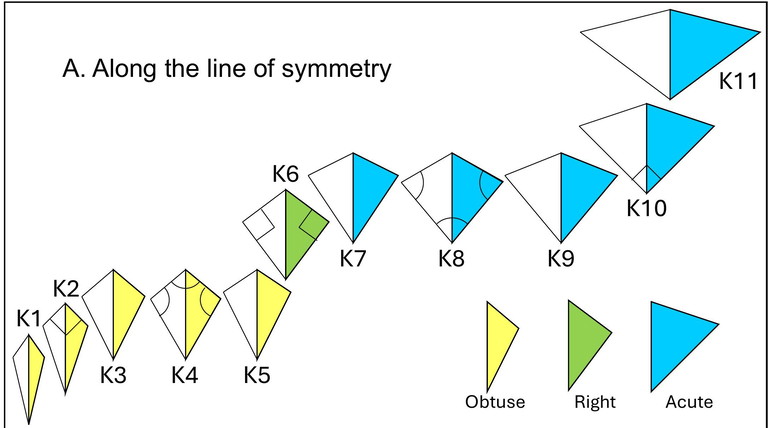
There are 11 types of kites (excluding rhombi) according to these pictures. K6 with 2 right angles is a special one, why? Can you characterise each of K1, K2… K11? Can you draw a kite for each of these 11 categories by specifying angles or sides-diagonals? Can you draw more than one for each category?
Is the halving diagonal (the line of symmetry) always the longer one? In “Diagonal-wise”, the 2 categories marked with stars can have equal diagonals. The blue star category K6 includes kites of all 3 kinds (i) halving diagonal longer, (ii) equal diagonals and (iii) halving diagonal shorter. The green star category K8 includes kites with the halving diagonal being the longer one, and when the diagonals are equal, it becomes a square!
Here are some questions students can explore.
A. Along the line of symmetry
1. What is the line of symmetry in each kite? 2. Why is it the line of symmetry?
3. Consider the triangles formed by the line of symmetry. Based on these triangles, in how many distinct groups can you classify K1, K2… K11? What are these groups?
4. These groups categorize the pair of equal (and opposite) angles of the kite. Can there be subgroups within each group? What do these subgroups categorize?
5. Optional: Can you form a tree diagram?
6. If we consider rhombi instead of kites, how many possibilities are there considering the triangles formed by a line of symmetry?
B. As sum of two isosceles triangles
1. Take any kite. Consider the common side of the two isosceles triangles.
How is this side related to the kite?
2. Consider all possible isosceles triangles – acute, right, obtuse. What are the possible combinations that generate: a. A kite b. A rhombus c. Any other special quadrilateral possible? Which one? 3. What would be the equal angles (acute/right/obtuse) of each such kite?
4. Classify K1, K2… K11 based on the classification in 2a. Can you find a kite outside K1, K2… K11?
C. Angle-wise
1. Consider the largest angle in any kite. What type of angle is it? 2. What type of angle is the smallest one?
3. A kite has a pair of equal and opposite angles. How many types of kites are there based on this pair?
4. Why does K2 have a light blue angle < the darker blue angle of K7?
5. Can you form a tree diagram classifying different types of kites based on the angles? Indicate where each of K1, K2… K11 are on this diagram.
6. Can you give examples for each of K1, K2… K11? E.g., K6: 120°90°-90°-60°
7. Can you find a kite with an angle combination outside K1, K2… K11?
8. Draw a K6 kite. Draw a circle with the halving diagonal (or line of symmetry) as the diameter. What do you observe? Do you observe the same for K1, K2... K5 or K7, K8… K11?
D. Diagonal-wise
1. Describe each of K1, K2… K11 in terms of the parts of the diagonal a, b and c. E.g., K2: a = c < b
2. Draw a kite for each of K1, K2… K11 using your choice of a, b and c. Ensure b > c.
3. Which diagonal is longer for K1, K2… K6? Which one for K9, K10 and K11? Why?
4. Find the relation among a, b and c if the diagonals of a kite are equal.
5. Now draw 3 K7 kites as follows:
a. Halving diagonal longer than the other one
b. Both diagonals equal
c. Halving diagonal shorter
6. Challenge: Prove that if the diagonals of a kite are equal then the equal (and opposite) angles must be acute.
MATH SPACE is a mathematics laboratory at Azim Premji University that caters to schools, teachers, parents, children, NGOs working in school education and teacher educators. It explores various teaching-learning materials for mathematics [mat(h)erials] their scope as well as the possibility of low-cost versions that can be made from waste. It tries to address both ends of the spectrum, those who fear or even hate mathematics as well as those who love engaging with it. It is a space where ideas generate and evolve thanks to interactions with many people. Math Space can be reached at mathspace@apu.edu.in