Problem Corner

KUMAR GANDHARV MISHRA

Picture yourself as a lab technician during a pandemic, faced with a critical challenge. Resources are scarce, and you need to identify which one of the 15 samples is contaminated with a virus. The catch? You have only 4 test tubes at your disposal, and you want to filter out negative samples using only these 4 test tubes in the most efficient manner. Can you detect the ‘poisoned’ sample?

This article is based on a hypothetical simulation activity to detect poisoned samples from a set of given bottles. What makes the situation interesting is that the number of samples is greater than the number of test tubes available for detecting poisoned samples. The simulation can be done either using spreadsheets or pen-and-paper, and provides an opportunity to learn binary arithmetic and explore different situations related to detecting samples.

The National Education Policy 2020 and the National Curriculum Framework for School Education 2023 emphasise computational thinking in the classroom. It has been described as one of the key 21st century skills in daily life. In simple words (see [1]), computational thinking involves describing a problem; identifying the important details needed to solve this problem; breaking down the problem into small and logical steps; using these steps to create a process that solves the problem; and evaluating this process. It uses algorithmic thinking, abstraction, decomposition, pattern recognition and generalisation, evaluation and logic to solve the problem at hand.

Keywords: Binary arithmetic, Computational thinking, Reasoning, Sample sorting

Computational thinking is also about thinking like a computer scientist, and when computers come in, how can binary numbers be left behind? Computers store information in the form of binary digits (bits), and understanding binary representation can help us understand the workings of computers because, at a fundamental level, computers are just machines for flipping binary digits on and off. Teaching binary numbers as an introduction to computational thinking introduces students to algorithms and decomposition, and during this process, they learn to break down the problems of calculating binary numbers and converting between binary and decimal numbers, into step-by-step processes. It also introduces abstraction, as students learn that two different things (0 and 1) can be used to represent any and all information (See [2]).

Keeping these points in mind, this article outlines an activity that involves distinguishing between two types of samples—positive and negative—within a larger set. During this activity, learners engage in computational thinking by using binary numbers to represent different samples and breaking down the problem into small steps. They apply reasoning and logic to determine the status of each sample based on the colour patterns displayed in test tubes. It also involves playing with computers using spreadsheets on Excel.

For simplicity, let’s assume we have a chemical indicator that reveals viral contamination by changing the colour of the sample. If the sample turns red, it indicates that the sample is poisoned, and we describe this result as ‘positive.’ Conversely, if the sample turns green, it shows that the sample is not poisoned, which we refer to as ‘negative.’ (Note that in this context, ‘negative’ means the sample is safe and unpoisoned).

Given that the number of test tubes is less than the number of samples, our goal is to efficiently filter out the negative samples, thereby reducing the testing burden significantly in the first step. Since four test tubes are insufficient to simultaneously test each of the 15 samples individually, the samples must be mixed within these four tubes. We capitalise on the fact that we have fifteen samples and four test tubes, By employing binary arithmetic, we can code the samples in such a way that allows us to identify those likely poisoned. Table 1 below shows the binary equivalents of decimal numbers up to 15. Using the binary coding system the samples can be represented as:

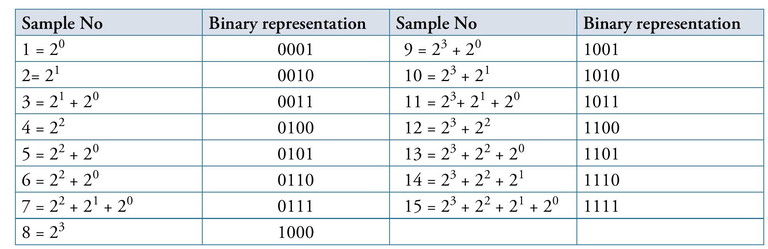
Table 1: Reading from right to left, a 0 is put where there is no power of 2 and a 1 where there is.

Each binary code also represents a unique way of putting a sample in these four test tubes according to its 4-digits. Let ‘1’ denote putting a sample into the corresponding test tube and a ‘0’ denote skipping the test tube. Let us denote the test tubes as T1, T2, T3 and T4. Now, for example, sample number 5, whose binary representation is 0101, can be put into the test tubes T2 and T4 (1 is at the 2nd and 4th position in binary code of 5), while sample number 6 (0110) can be put into T2 and T3 and so on. Each sample can be put in at least one test tube and at most 4 test tubes. For instance, sample number 1 will be put in only one test tube, and sample number 15 will be put in all 4 test tubes. If a test tube turns green, it means all samples put in this tube are negative. On the other hand, if a test tube turns out red then it doesn’t mean that all samples related to it are positive, that test tube can turn red even due to one positive sample put in it. So, in a way, the green signal helps us filter all those samples which were put in that test tube.

Let’s take a case where two of the test tubes indicate at least one positive sample in them.

Figure 1: Results obtained in 4 test tubes.

Here test tubes T1 and T3 turn green, while T2 and T4 turn red. This result conclusively identifies all samples placed in either T1 or T3, or both, as negative, given that the binary ‘1’s for these samples correspond to the green test tubes. Referring to Table 1, we can conclude that :

• T1 is green: All samples placed in T1 are negative, which corresponds to samples that have a binary ‘1’ in the first position—specifically, samples 8 to 15.

• T3 is green: Similarly, all samples placed in T3 are negative, corresponding to samples with a binary ‘1’ in the third position—samples 2, 3, 6, 7, 10, 11, 14 and 15.

On the other hand, the samples placed in T2 and T4 are suspected of being positive. However, it doesn’t mean that each sample put into these test tubes is positive. Each sample put in T2 (4, 5, 6, 7, 12, 13, 14 & 15) can be positive or at least one is positive for sure, the same goes for T4 ( 1, 3, 5, 7, 9, 11, 13, 15). Comparing with the conclusions from the green test tubes, we filter out the negative samples (3, 6, 7, 9, 11, 12, 13 14, 15) and reduced our task to identify the provisionally (those samples which are considered to be positive unless and until proven negative) positive samples (1, 4, 5), which we can re-test.

Some noteworthy points: The test tube colour combination shouldn’t be related to similar appearing binary code and the respective decimal number. For example, the pattern of the test tube for positive result in Figure 1 appears as 0101 which matches with the code of sample number 5, but sample number 5 may be negative. T2 and T4 can show positive results not only because of sample 5, but also because of other samples which have been put in these test tubes. For example, one positive sample in T2 and one positive sample in T4 can make the test tube combination positive, while sample number 5 could be negative.

Suppose according to the test results T4 is green and T1, T2 and T3 are red.

What would be your conclusion?

The teacher can convert the above binary-based reasoning into an in-class activity involving a series of tasks.

1. The teacher introduces the problem at hand and provides an illustration.

2. The students are asked to fill the following table depicting the binary representations of sample numbers and which of the 15 samples are put into each of the 4 test tubes. (We illustrate for sample number 6 here)

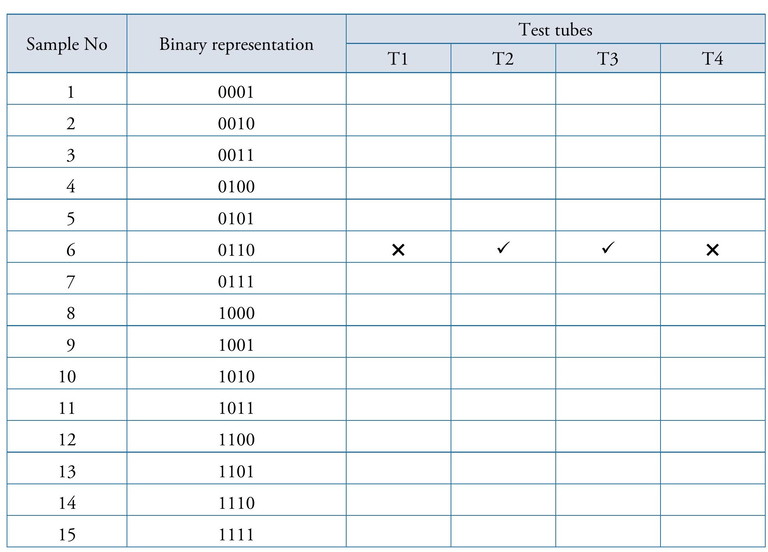
Table 2

3. The students are asked to count how many combinations of test results are possible.

4. The students are divided into pairs and assigned a few particular test results (by lottery) given as coloured strips (two distinguishable colours – say, red and green). They are instructed to try to filter out the negative samples based on the test tube colour combinations they got.

5. The teacher demonstrates for a sample. If the given colour strip has T1 and T3 in red colour, and T2 and T4 in green colour as in Figure 3, the teacher explains how to filter out the negative samples and record them in the table generated by the students (Figure 2).

Figure 2

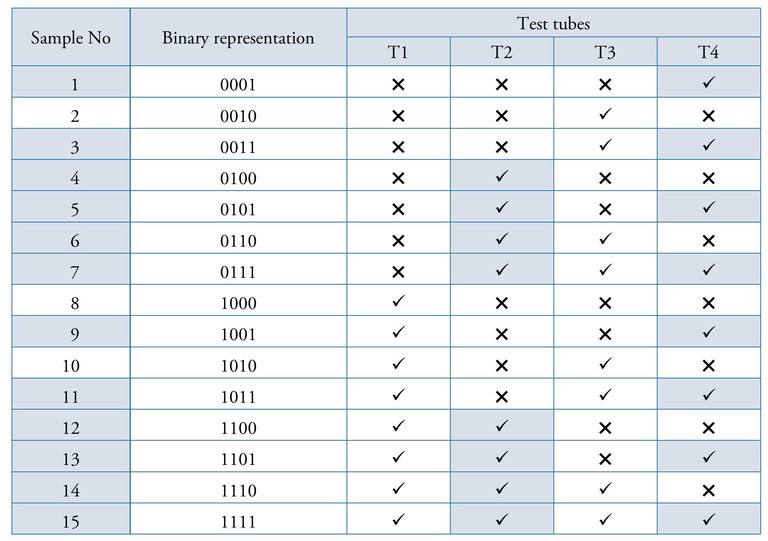
Table 3

In this case, the negative samples are 1, 3, 4, 5, 6, 7, 9, 11, 12, 13, 14 and 15. The teacher then proceeds to explain how to find the positive samples. In this case, the only remaining samples are 2, 8 and 10. These samples can be renumbered as I, II, and III respectively and tested again using test tubes T1, T2 and T3 alone. The students are asked to draw possible outcomes if only one of these samples is poisoned.

6. The students work in pairs and record their results. In the middle of the activity, any two groups which got the same test result could share their conclusions. At the end of the activity, the teacher randomly picks a few pairs and asks them to share their findings with the class.

7. The students are provided with a worksheet to work on further.

To make the activity tactile, the students can divide themselves into pairs and generate all 16 possible test results as colour patterns (as in Figure 4) and put them in a bowl. Each pair can draw one cutout from the bowl and do the prescribed activity. This activity reinforces the computational thinking aspects by decomposing the problem into small steps and using logic detecting the negative samples and probable positive samples.

Suppose T1, T2, T3 turn green, and T4 turns red (Figure 3).

Figure 3

How would you proceed?

1. Suppose that sample number 15 is poisoned. What would be the result you should expect? Indicate the colours of the test tubes.

2. If sample number 15 is poisoned, how will you identify it? 3. If you have five test tubes, up to how many samples can you test? What about six test tubes? 4. How many test tubes are required to test 1000 samples? Why?

5. In the following situations, calculate the number of provisionally positive (Those samples which are probable of being positive i.e. positive unless and until proved to be negative) samples.

Table 4

Converting the reasoning task into an activity using a simulation

This activity can be transformed into a simulation activity for students using Excel spreadsheets.

Let’s explore the different colour permutations of test tubes through Excel and the random function generator:

1. Open an Excel file spreadsheet and select any cell.

Figure 4

2. Use ‘=CHOOSE (RANDBETWEEN (1,2), “positive”, “negative”)’ function at the cell. With the selection key on the cell, expand the selection up to four cells horizontally. The terms ‘positive’ and ‘negative’ will appear in these four cells. Consider these 4 cells as 4 test tubes.

Figure 5

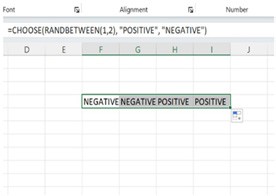
Figure 6

3. Select a cell other than these cells. Write any letter or number in this cell and press enter. You will observe that the words in the four cells change. Repeat this process by entering any number in any other cell; again, you will observe that the terms positive and negative vary in these 4 cells.

Figure 7

4. Now, select the 4 cells (test tubes) and using conditional formatting (highlight the cell that contains a specific text) label the cells with red colour and green colour (red for positive and green for negative).

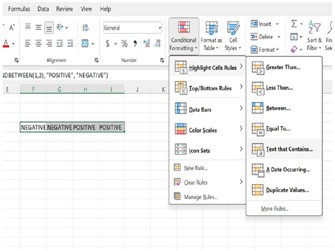
Figure 8

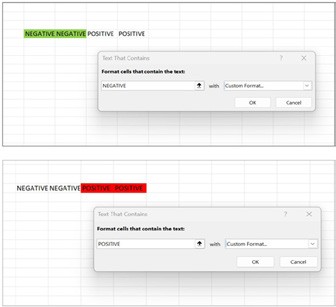
Figure 9

5. Reduce the font size of terms ‘positive’ and ‘negative’ as small as possible; say up to size 1 so that only colours appear on the test tube cells and the numbers get diminished.

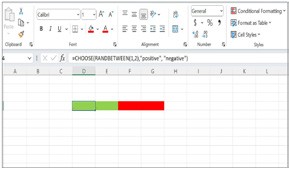
Figure 10

6. Select any other cell and write any number and press enter, the colour of the test tube cell changes. By doing this you can get different permutations of colour in the test tube cells. Some examples of possible permutations:

Figure 11

7. Consider the red cells as an indicator of positive/poisoned (provisional) samples put in them and green cells as an indicator of negative samples put in them. So, a total of 24 i.e., 16 colourful permutations can be generated. Among these 16 permutations, one of the permutations can refer to all 4 test tubes with zero i.e., skipping all test tubes. So, we don’t need to focus on this situation, but on the rest of the 15 situations.

8. Create the table using spreadsheets, depicting the relationship between 15 samples and 4 test tubes.

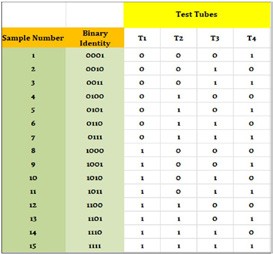
Figure 12

Now, we will use the same reasoning as shown in Figure 12.

During the whole process, students use reasoning and logic to decompose the task of distinguishing the samples (positive or negative as red or green) by filtering out negative samples and again working with the smaller lot. The student engages with binary arithmetic when he/she gives identity to each sample, looks for patterns among the test tubes and evaluates his/her decision of labelling a sample as negative or provisionally positive. This is what computational thinking is all about in this activity, where the teacher provides an opportunity for the student to decompose the problem into small steps with logic and devise his/her algorithm to solve while playing with binary numbers.

Author’s note: A similar approach to test Covid-positive samples through binary arithmetic also appeared as a suggestion by Kadri (2020), but it used the concept of ratio of mixing of samples.

Acknowledgement: The author is grateful to the reviewers for their valuable suggestions.

1. CS Unplugged.(n.d.). Retrieved from Computational thinking: https://www.csunplugged.org/en/csunplugged.org/en/1.

2. CS Unplugged.(n.d.). Retrieved from Binary numbers: https://www.csunplugged.org/en/topics/binary-numbers/whats-it-all-about/

3. Houston, K. (2016, December 15). Can you solve the poison wine challenge? Retrieved from PBS Infinite Series: https://www.youtube.com/watch?v=N3qmN6pYhi0

4. Kadri, Usama. “The Maths Logic that could help test more people for Coronavirus.” The Conversation, April 9, 2020. https://theconversation.com/the-maths-logic-that-could-help-test-morepeople-for-coronavirus-134287.

5. Ministry of Education. (2020, July 29). National Education Policy 2020. Retrieved February 29, 2024, from Ministry of Education: https://www.education.gov.in/sites/upload_files/mhrd/files/NEP_ Final_English_0.pdf

6. National Council of Educational Research and Training. (2023). National curriculum framework for school education 2023. Retrieved from National Council of Educational Research and Training: https://www.ncert.nic.in/pdf/NCFSE-2023-August_2023.pdf

KUMAR GANDHARV MISHRA is a PhD Research Scholar (Mathematics Education) at the Central University of South Bihar. He completed his Masters in Mathematics Education-M.Sc. (Mathematics Education) from Cluster Innovation Centre, University of Delhi. He has also worked with Center for Creative Learning, Indian Institute of Technology Gandhinagar in the field of STEM education. He often writes on social and cultural aspects of mathematics, and mathematics education. He can be reached at mishrakumargandharv@gmail.com