ARUNI JOSEPH

This article shares my experiences of teaching in a government school in rural Rajasthan (Oct-Nov 2022) as part of the field practice of my M.A. Education programme at Azim Premji University. The experience in the field helped me understand the difficulties children face specifically in understanding mathematical concepts. I observed and attempted to address the challenges children faced in understanding angles in different orientations and in the measurement of angles. There was a scarcity of concrete materials which are very crucial for the teaching-learning of geometry and textbooks were used as the sole resource for teaching. A few pedagogical practices that were tried in order to address these concerns and which were found to be effective are discussed here.

Through geometry, children develop the power to imagine, discern elements that are not shown, visualise objects as dynamic and recognise facts and relationships that can be established (Johnston-Wilder, 2005). As per the theory of Pierre and Dina van Hiele, children progress through levels of geometric thinking (van Hiele, 1986). From the initial level of judging a figure by its appearance, children will identify the properties associated with the figures. After that, they draw relationships between properties and find one from the other. In the end, children will learn to reason in a formal mathematical way. Table 1 gives Van Hiele’s levels of learning geometry.

Keywords: Geometry, Angles, Conceptual Understanding, Mathematics TLM, Games.

I conducted over 25 sessions of 40 minutes duration each, for a class of 35 children in Grade 7. This was at the Mahatma Gandhi Govt School, Paldi-M in the Sirohi district of Rajasthan. Definition of angles, types of angles such as obtuse angles, measurement and drawing of angles using a protractor had already been taught to the children. The following were the observations made during the initial days:

• 25% of the children faced difficulty in understanding angles in different orientations.

• 70% of the children had challenges in angle measurements using a protractor.

• 5 children were found to be disinterested in doing paper and pen work in class.

• Children were not exposed to any teachinglearning materials for angles.

To address the difficulties faced by the children, a few pedagogical practices were tried which included the use of concrete materials and the extension of the content in the textbook. These served as a vehicle to transact the topics of angle representation, angle measurement, angle pairs such as complementary and supplementary angles, and angle pairs formed when a transversal cut a pair of parallel lines.

TLMs can be effective in helping children navigate the abstraction in angles. Learning how to represent angles mathematically is not straightforward for young children, even though angles occur everywhere in their daily life (Watson, 2013). A few materials tried in the class are given below, mostly made of recyclable materials like newspapers.

Most of the time, our teaching focuses on visualising angles formed when two lines/ line segments intersect. There is evidence that children are more aware of angle in the context of movement (turn) than in other contexts and learn about the mathematics relatively easier in this context (Nunes, 2009).

Figure 1

Paper fans (Figure 1) were made using ice-cream sticks and newspapers and were used to show angle in the context of movement. Children did the activity in groups of 5 members. They were told to describe what they saw while using the fans. They formed different types of angles and described them. “This is more than 90° and is an obtuse angle.”

They used angles in different orientations unknowingly as they used the fans. A few questions were asked to assess their learning. For example, an obtuse angle was shown to the class. Children recognised it as an obtuse angle. Thereafter, the orientation of the angle was changed without changing the measurement and they were asked what type of angle that was. Suman, who used to be very quiet in class, said it was an obtuse angle. When asked why it was so, her reply was, “You did not change the positions of the sticks, you just turned it upside down. So, it is the same angle.” The group activity encouraged engagement and discussion among children. Classroom tasks can be used to give children opportunities to explain, justify and be critical of their own and peers’ explanations (Watson, 2013).

Many children find it challenging to measure the angle in a given figure, especially when the figure is in an uncommon orientation. 360° handmade protractor (Figure 2) was used as a visual aid to form angles and measure them at the same time. This also gave the opportunity to explore angles greater than 180° which is a limitation of the conventional protractor. This material with two hands was made using chart papers and secured using a pin and a sponge piece. Children explored this material in groups of four members and were asked to make angles of different types and measures.

Figure 2

They described what they made. “This is 120° and is an obtuse angle”, “When we make an obtuse or an acute angle, we also get a reflex angle at the other side”. When asked to show 30° angles in three different ways, some of the responses given are shown in Figures 3, 4 and 5. After these activities, there was a noticeable improvement in measuring and drawing angles using protractors.

Figure 3

Figure 4

The model in Figure 7 was used to find relations between angles formed when a transversal cuts pair of parallel lines. For example, what can we say about the measures of ∠AXP and ∠CYX? What about ∠AXY and ∠DYX? Once children articulated the relationship, we moved towards learning their universally accepted names - corresponding angles and alternate interior angles respectively.

Figure 5

In groups, children were asked to explore and identify angles around the transversal cutting two lines. Children concluded that there were eight angles in such a scenario.

Figure 7

The model’s orientation was changed (Figure 8) to check if children identified the pair of angles they worked with earlier, and their relationship. Children could make out that the change in orientation did not change the measure of the angles or the relationship between specific pairs of angles.

Figure 6

Figure 8

A few activities and guiding questions were prepared using NCERT textbooks.

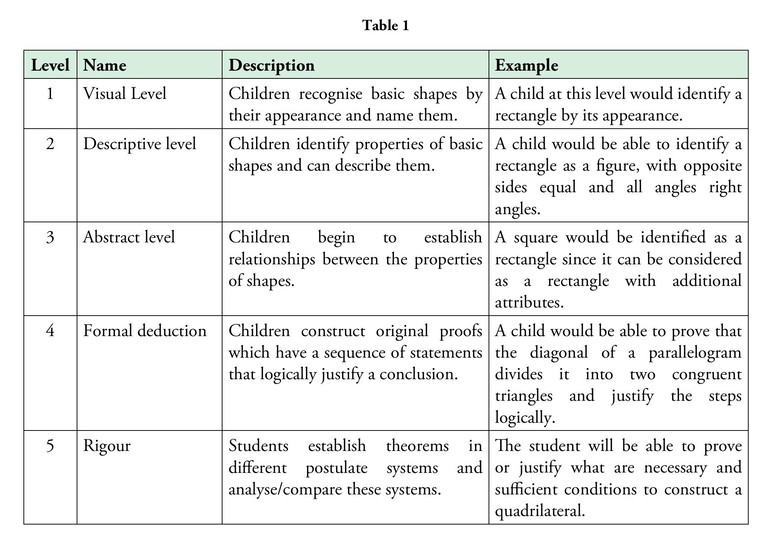
One such activity was on complementary and supplementary angles. Children were divided into 2 groups. Pictures of different measures were given to the children of one group (Figures 9, 10, 11, 12). They had to find the complement or supplement of each angle which was with the children of the other group.

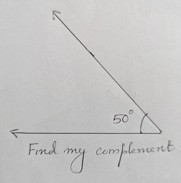
Figure 9

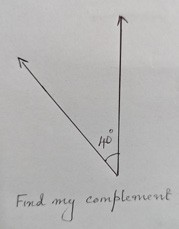
Figure 10

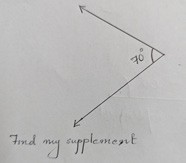
Figure 11

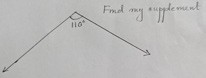
Figure 12

Children were engrossed in the activity by calculating, estimating and verifying with the pictures. This activity was found to be beneficial for children who were not interested in paper and pen work. Post the activity, children were asked to describe what they saw in the angle pairs. This was to understand whether they saw the sum of the angle pairs as 180° and 90°, and hence could differentiate between supplementary and complementary angles respectively.

Guiding questions were used to enable children to apply higher-order cognitive skills and to prepare them for formal mathematical thinking in secondary school. The angles that came alive would be more meaningful when they saw their application in a different context. Table 2 has a few such scenarios tried in 7th grade and based on content from the 9th grade NCERT textbook. To do these, students would need to know representation and types of angles, angle pairs such as supplementary and complementary angles, as well as angle pairs formed when a transversal cuts a pair of parallel lines.

Children would get the opportunity to use higher-order skills such as applying and evaluating from activities like these. When children are asked to find solutions in groups, it becomes an exploratory activity, making them think, propose, make mistakes and learn. A geometry teacher can thus accelerate children’s progression in the VanHiele model. Classroom tasks should provide opportunities for students to develop problemsolving skills and engage in problem-posing (Watson, 2013).

• Manipulatives such as paper fans and 360° protractors were found to be effective in giving children exposure to angles in the context of movement, angles in multiple orientations and angles as relational measures. There was a noticeable improvement in the measurement and construction of angles using protractors after this.

• 360° protractors can be used in overcoming the limitations of a conventional protractor where angles more than 180° cannot be shown. If made using transparent sheets this can also be used for measuring and drawing angles.

• Introducing games and guiding questions encouraged inquisitiveness in children, thus making learning joyful and participative.

• Giving children opportunities to explore using concrete materials and effective textbook usage accelerated their progression in van Hiele’s model of learning geometry.

References

1. Clements, D. H. (2003). Chapter 11. Teaching and Learning Geometry. In A Research Companion to Principles and Standards for School Mathematics. NCTM

2. Johnston-Wilder, S., & Mason, J. (2005). Developing thinking in geometry (pp. 209-211). Open University in Association with Paul Chapman Pub.

3. Nunes, T., Bryant, P., & Watson, A. (2009). Paper 5. Understanding space and its representation in mathematics. In Key understandings in mathematics learning. Nuffield Foundation. London.

4. Van Hiele, P.M. (1986). Structure and insight: a theory of mathematics education. Academic Press. Orlando.

5. Watson, A., Jones, K and Pratt, D. (2013). Chapter 5. Spatial and geometrical reasoning. In Key ideas in teaching mathematics: research-based guidance for ages 9-19 (pp. 92-116). OUP.

6. NCERT Mathematics textbooks for grades 7 and 9.

Aruni Joseph arunipradeep@gmail.com started her career as an IT professional. After spending a decade in the industry, she moved on to pursue her interest in teaching Mathematics by taking after-school tuitions. She completed her M.A. in Education from Azim Premji University in 2023. After that she worked with the Gubbachi Learning Community in Bengaluru, teaching Mathematics to the out-of-school children of migrant labourers. Currently she works in Prakriya Green Wisdom School, Bengaluru. Aruni may be contacted at

Euclid’s postulates, Elements’ true signature, Akin to nature’s basic elements, a divine scripture.

Euclid’s five, building blocks to Geometry, Nature’s five mirror our being’s symmetry.

Two points uniquely determine a straight line, Extend indefinitely, a terminated line’s design. Circles constructed, varied in size and location, Congruent right angles, Euclidean geometry’s foundation.

The fifth, the Parallel postulate, sparked a mathematical divergence, Paving a way to non-Euclidean geometry’s emergence.

A traditional shift, where parallels take an unusual stance, In hyperbolic and elliptic realms, mathematical refinement enhance.

Euclidean geometry initiated through Euclid’s sage, Riemann’s elliptic geometry, an elegant grace.

Lobachevsky, Bolyai, and Gauss in hyperbolic fervour, A tribute to minds with questioning valour.

Composed by: Ravindra K Bisht

Department of Mathematics, NDA, Khadakwasla, Pune,India